What is a fractal? The Laymen’s Guide

A fractal is simply a shape whose blueprint repeats at every scale—an infinite “copy-paste” of itself. What does self-similarity mean in practice? Let’s dissect the Sierpiński Triangle.

To construct a Sierpiński Triangle, start with one solid triangle. Attach two identical triangles so that they meet at one corner—hello, triforce. Then take two triforces, align their vertices in the same way, and repeat ad infinitum.

What emerges is a pattern of ever-smaller triangles carved out of the original—a textbook case of self-similarity.

How Fractals are generated

You don’t need to explicitly tile smaller copies to get a fractal. Some algorithms use randomness and simple arithmetic to conjure up the same pattern. For example, here’s a “chaos game” that also yields the Sierpiński Triangle (lifted, maybe, from Wikipedia):

1. Take three points in a plane to form a triangle.
2. Randomly select any point inside the triangle and consider that your current position.
3. Randomly select any one of the three vertex points.
4. Move half the distance from your current position to the selected vertex.
5. Plot the current position.
6. Repeat from step 3.

At first glance, these six steps look arbitrary—how can random midpoints produce an ordered fractal? Yet after a few thousand iterations, the Sierpiński pattern crystallizes out of apparent chaos. It seems almost paradoxical that such a minimal rule set yields perfect self-similarity. And if you thought that was neat, wait until you meet the Mandelbrot Set—exactly why this blew my pants off the first time I saw it.

The Mandelbrot Set

Benoit Mandelbrot was a Polish mathematician who, in the late ’70s, started probing Julia-set fractals. His work culminated in Fractals: Form, Chance and Dimension, which codified the modern study of fractals.

"I never had the feeling that my imagination was rich enough to invent all those extraordinary things on discovering them. They were there, even though nobody had seen them before. It's marvelous, a very simple formula explains all these very complicated things." – Benoit Mandelbrot

A Formal Definition

In technical terms, the Mandelbrot Set consists of every complex number \(C\) for which the iteration below remains bounded as \(N \to \infty\). Here \(Z_0=0\) and we repeat forever:

A quick aside: Complex Numbers

Despite the intimidating name, complex numbers are just 2-D coordinates. On the real line you need one number; on a plane you need two—an \(X\) and a \(Y\):

\((X, Y)\)

Likewise, a complex number combines a real part and an imaginary part (written with \(i\), or \(j\) in electrical engineering):

This represents the point \((2.3, 7)\) in the plane. But don’t treat the real and imaginary parts as separate arithmetic chores—the pair as a whole defines the number. (For a deep dive on how complex addition and multiplication work, see 3Blue1Brown.)

Back to Mandelbrot

Revisiting our definition:

Any complex number \(C\) where the following equation, applied \(N\) number of times, is bounded. And where \(Z_{0}=0\) and \(N=\infty\)

Still with me? Choose a complex number and iterate:

Then apply:

After five rounds, \(-63-118i\) is already huge, and it only grows further—so \(1+2i\) escapes to infinity and isn’t in the set.

Now try a point that doesn’t run away:

\begin{align*} C &= .25-.3i \\ Z_{0} &= 0 \\ Z_{1} &= Z_{0}^{2}+C=.25-.3i \\ Z_{2} &= Z_{1}^{2}+C=.223+.45i \\ Z_{3} &= Z_{2}^{2}+C=.097+.5i \\ Z_{4} &= Z_{3}^{2}+C=.009+.397i \\ Z_{5} &= Z_{4}^{2}+C=.092+.307i \\ \vdots \\ \lim_{N \to \infty} Z_{n+1}&=Z_{n}^{2}+.25-.3i=? \end{align*}

Here, the values hover in a tight region—they stay bounded. That’s the hallmark of membership in \(M\).

It’s okay if you skipped the previous part

The payoff comes when you visualize the result across the complex plane: color each point black if it belongs to M, or assign a hue based on how quickly it escapes. The canonical image emerges:

Under a typical escape-time rendering you’ll immediately spot the main cardioid—that large, heart-shaped bulb—and its attached periodic bulbs (period 2, 3, 4, etc.) spiraling off. Each bulb’s interior corresponds to points whose iterations cycle with a fixed period.

Zoom in on the jagged boundary and you’ll discover much more detail within:

What about colors?

Colorful renderings exploit escape time: record the iteration count \(n\) when \(|Z_n|\) exceeds a threshold (usually 2). Map \(n\) to a gradient—rapid escapes might glow red, while slow ones drift through cooler blues. The result is a heatmap of complex dynamics, painting the subtle pace at which each point “blows up.”

Final Thoughts

From Sierpiński’s triforces to the bound-and-unbound dance of the Mandelbrot Set, fractals prove that iteration plus recursion equals infinite complexity. If that idea resonates, consider this: I’ve carried that very principle on my skin. Below the surface of my arm sits the formula

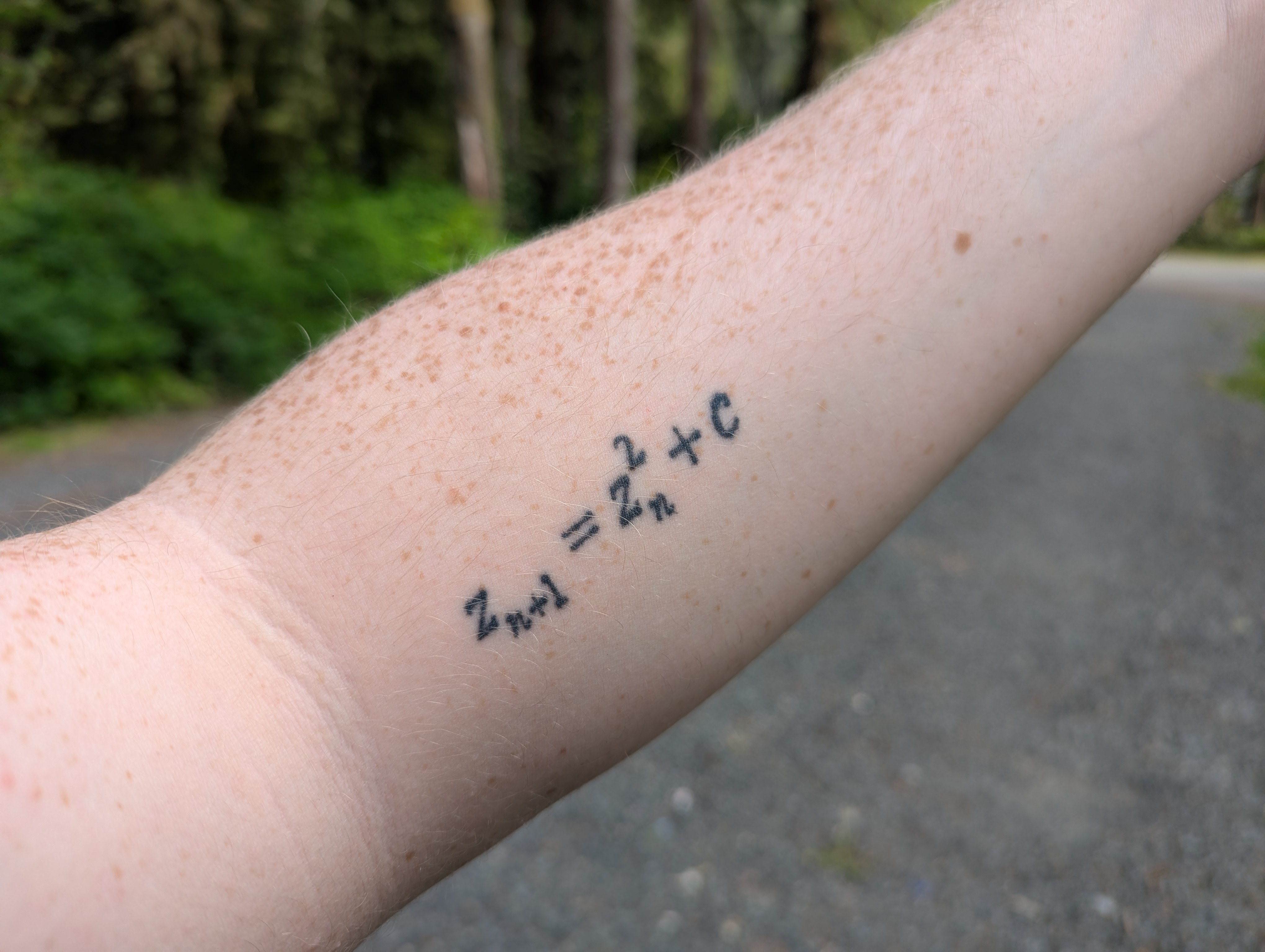
—my permanent reminder that a single, deceptively simple line of math can generate unending wonder.